Java – How to Create a Binary Search Tree

• What is a binary search tree?
• What are different kind of traversals?
• Code Samples

What is a binary search tree?

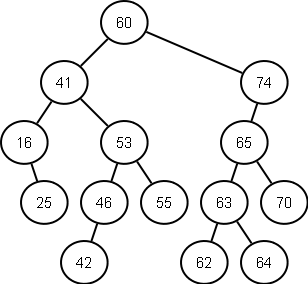
A binary search tree is a binary tree in which every node contains a key that satisfies following criteria:

• The key in left child is less than the key in the parent node
• The key in the right child is more than the parent node
• The left and right child are again binary search trees.

Following diagram represents a binary search tree:

What are different kind of traversals?

Following are three different kind of traversals:

• Preorder traversal: In preorder traversal, the node is visted first and then, left and right sub-trees.
• Inorder traversal: In inorder traversal, the node is visited between left and right sub-tree.
• Postorder traversal: In postorder traversal, the node is visited after left and right subtrees.

Code Sample – How to Create a Binary Search Tree

If the numbers such as {20, 15, 200, 25, -5, 0, 100, 20, 12, 126, 1000, -150} are to be stored in a BinaryTree (represented by code below), following would get printed using different kind of traversal mechanism:

		//Preorder traversal
		20, 15, -5, -150, 0, 12, 200, 25, 20, 100, 126, 1000

		// Inorder traversal
		-150, -5, 0, 12, 15, 20, 20, 25, 100, 126, 200, 1000

		//Postorder traversal
		-150, 12, 0, -5, 15, 20, 126, 100, 25, 1000, 200, 20

Following is the code for creating binary tree that uses following BinaryTree class and traversals:

		BinaryTree tree = new BinaryTree( 20 );
		int[] nums = {15, 200, 25, -5, 0, 100, 20, 12, 126, 1000, -150};
		for(int i : nums ) {
			tree.addNode( i );
		}
		
		tree.traversePreOrder();
		tree.traverseInOrder();
		tree.traversePostOrder();

Following is the code for BinaryTree class:

	public class BinaryTree {

	private int data;
	private BinaryTree left;
	private BinaryTree right;

	public BinaryTree(int num) {
		this.data = num;
		this.left = null;
		this.right = null;
	}
	// As a convention, if the key to be inserted is less than the key of root node, then key is inserted in
	// left sub-tree; If key is greater, it is inserted in right sub-tree. If it is equal, as a convention, it 
	// is inserted in right sub-tree
	public void addNode(int num) {
		if (num < this.data) {
			if (this.left != null) {
				this.left.addNode(num);
			} else {
				this.left = new BinaryTree(num);
			}

		} else {
			if (this.right != null) {
				this.right.addNode(num);
			} else {
				this.right = new BinaryTree(num);
			}

		}
	}
	// Visit the node first, then left and right sub-trees
	public void traversePreOrder() {
		System.out.println( this.data );
		if( this.left != null ) {
			this.left.traversePreOrder();
		}
		if( this.right != null ) {
			this.right.traversePreOrder();
		}
	}
	// Visit left sub-tree, then node and then, right sub-tree
	public void traverseInOrder() {
		if( this.left != null ) {
			this.left.traverseInOrder();
		}
		System.out.println( this.data );
		if( this.right != null ) {
			this.right.traverseInOrder();
		}
	}
	// Visit left sub-tree, then right sub-tree and then the node
	public void traversePostOrder() {
		if( this.left != null ) {
			this.left.traversePostOrder();
		}
		if( this.right != null ) {
			this.right.traversePostOrder();
		}
		System.out.println( this.data );
	}

}